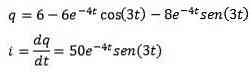That change from Laplace has in recent years been very important in the study of engineering, mathematics, physics, among other scientific fields, as well as being of great interest in theory, providing a simple way to solve problems originating from science and engineering.
Initially the Laplace transform was presented by Pierre-Simon Laplace in his study of probability theory and was initially treated as a mathematical object of only theoretical importance ..

The current application arises when various mathematicians try to provide formal justification for the “operational rules” used by Heaviside in the study of electromagnetic theory equations.
Index
- 1 Definition
- 1.1 Example
- 1.2 Theorem (Adequate conditions for existence)
- 1.3 Laplace transform of some basic functions
- 2 History
- 2.1 1782, Laplace
- 2.2 Oliver Heaviside
- 3 Properties
- 3.1 Linearity
- 3.2 The first translation theorem
- 3.3 The second translation theorem
- 3.4 Changes in scale
- 3.5 Laplace transform derivatives
- 3.6 Laplace integral transformation
- 3.7 Doubling by tn
- 3.8 Division by t
- 3.9 Periodic functions
- 3.10 Behavior F (s) when s tends to be infinite
- 4 Reverse transformation
- 4.1 Exercise
- 5 Laplace transformation application
- 5.1 differential equations
- 5.2 System of differential equations
- 5.3 Mechanics and electrical circuits
- 6 References
Definition
Let f be the function defined for t ≥ 0. Laplace transform is defined as follows:
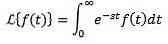
It is said that the Laplace transform exists if the integrals previously met, if not then it is said that the Laplace transform does not exist.
In general, to indicate the function you want to change, lowercase letters are used and uppercase letters correspond to transformations. In this way we will have:
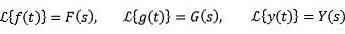
Example
Consider the constant function f (t) = 1. We have the transformation is:
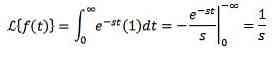
Every time the integrals meet, it’s always provided that s> 0. If not, s <0, la integral is diverge.
Let g (t) = t. Your Laplace transform was given by
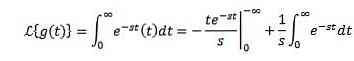
By integrating by parts and knowing that you -st it tends to 0 when t tends to infinity and s> 0, along with the previous example we have it:
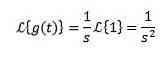
Transformations may or may not exist, for example the function f (t) = 1 / t integral that defines the Laplace transform is not integrated and therefore the transformations do not exist.
An adequate condition to ensure that the Laplace transformation of the function f exists, is that f is continuous in parts for t ≥ 0 and from the exponential sequence ..
It is said that a continuous function in parts for t ≥ 0, when for each interval [a, b] with a> 0, there is a finite number of points t k, where f has discontinuity and continuous in each subinterval [t k- 1 , t k ].
On the other hand, it is said that an exponential sequence function c if there are real constants M> 0, c and T> 0 such that:
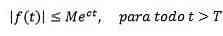
For example we have that f (t) = t 2 is an exponential order, because | t 2 | <e 3t for all t> 0.
Formally we have the following theorem
Theorem (Adequate conditions for existence)
If f is a continuous function per part for t> 0 and an exponential sequence of c, then there is a Laplace transform for s> c.
It is important to underline that this is a sufficient condition, that is, there could be a case that there is a function that does not fulfill this condition and even then the Laplace transform exists.
An example is the function f (t) = t -1/2 which is not continuous in the part for t ≥ 0 but the Laplace transform exists.
Laplace transform of some basic functions
The following table shows the Laplace transformation of the most common functions.

History
Laplace’s transformation owes its name to Pierre-Simon Laplace, a French mathematician and theoretical astronomer who was born in 1749 and died in 1827. His fame was such that he was known as Newton of France.
In 1744 Leonard Euler devoted his studies to integral with form
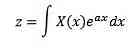
as a solution to ordinary differential equations, but quickly left this investigation. Later, Joseph Louis Lagrange, who greatly admired Euler, also investigated this integral type and related it to probability theory.
1782, Laplace
In 1782 Laplace began to study these integrals as solutions to differential equations and according to historians, in 1785 he decided to reformulate the problem, which later gave birth to Laplace’s transformation as understood now ..
After being introduced to the field of probability theory, it was not of interest to scientists at the time and was only seen as a mathematical object that was only theoretically interesting ..
Oliver Heaviside
It was in the mid-nineteenth century when British engineer Oliver Heaviside discovered that differential operators could be treated as algebraic variables, thus giving their modern application to Laplace transforms.
Oliver Heaviside was a British physicist, electrical engineer and mathematician who was born in 1850 in London and died in 1925. While trying to solve the problem of differential equations applied to vibration theory and using Laplace’s study, he began to form modern applications of Laplace’s transformation.
The results exhibited by Heaviside spread quickly throughout the scientific community at the time, but because his work was not rigorous, he was quickly criticized by traditional mathematicians ..
However, the usefulness of Heaviside’s work in solving physics equations made his method popular among physicists and engineers.
Despite this setback and after several decades of unsuccessful attempts, in the early 20th century a strict justification for the operational rules given by Heaviside can be given ..
This effort paid off thanks to the efforts of various mathematicians such as Bromwich, Carson, van der Pol, among others …
Property
Among the properties of the Laplace transformation, the following stands out:
Linearity
Let c1 and c2 be functions of constants and f (t) and g (t) for which Laplace transforms are F (s) and G (s), then we must:
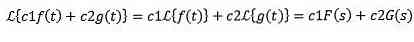
Because this property is said that the Laplace transform is a linear operator.
Example
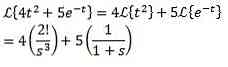
The first translation theorem
If it happens:
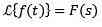
And ‘a’ is a real number, then:
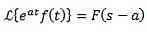
Example
As a Laplace transform of cos (2t) = s / (s ^ 2 + 4) then:
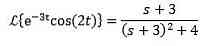
The second translation theorem
Yes
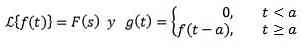
Then
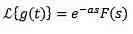
Example
If f (t) = t ^ 3, then F (s) = 6 / s ^ 4. And therefore, transformation
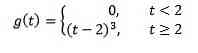
is G (s) = 6e -2s / s ^ 4
Change the scale
Yes
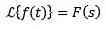
And ‘a’ is real not zero, we have to
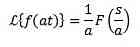
Example
Because the transformation from f (t) = sin (t) is F (s) = 1 / (s ^ 2 + 1) it must
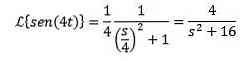
Laplace transform information
If f, f ‘, f “, …, f (n) are continuous for t ≥ 0 and exponential sequences and f (n) (t) are continuous in parts for t ≥ 0, then
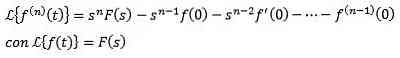
Integral transformation of Laplace
Yes
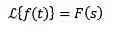
Then
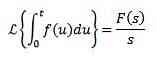
Multiplication with t n
If you have to
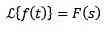
Then
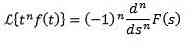
Division by t
If you have to
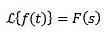
Then
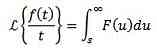
Periodic function
Let f be a periodic function with a period T> 0, that is, f (t + T) = f (t), then
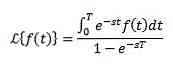
The behavior of F when s tends to be infinite
If f is continuous in parts and exponential order and
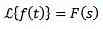
Then
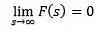
Reverse Transformation
When we apply the Laplace transform to the function f (t), we get F, which represents that transformation. In the same way we can say that f (t) is an inverse Laplace transform of F (s) and is written as
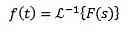
We know that the Laplace transformation of f (t) = 1 and g (t) = t is F (s) = 1 / s and G (s) = 1 / s 2 respectively, therefore we must
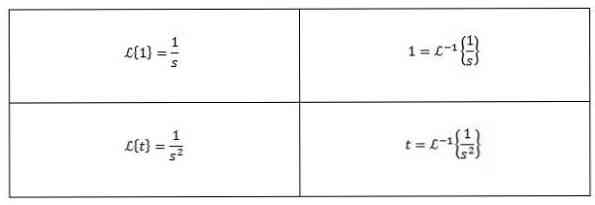
Some common Laplace inverse transformations are as follows

In addition, the Laplace inverse transformation is linear, that is, fulfilled
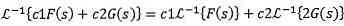
Exercise
Find out
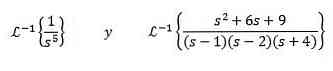
To complete this exercise we must match the function F (s) with one of the previous tables. In this case, if we take n + 1 = 5 and use the linearity property of the inverse transform, we multiply and divide by 4! Got
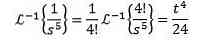
For the second inverse transformation we apply a partial fraction to rewrite the function F (s) and then the linearity property, obtain
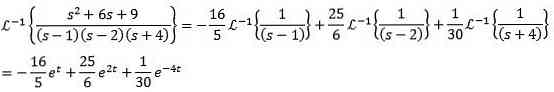
As we can see from these examples, it is common that the function F (s) evaluated is not exactly the same as one of the functions given in the table. For these cases, as observed, simply rewrite the function until it reaches the appropriate form.
Laplace transformation application
Differential equation
The main application of Laplace transformation is to solve differential equations.
Using the properties of the derivative transformation is clear
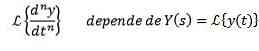
And from n-1 derivatives evaluated at t = 0.
This property makes transformation very useful for solving initial value problems where differential equations with constant coefficients are involved.
The following example shows how to use Laplace transform to solve differential equations.
Example 1
The following initial value problems are given
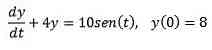
Use Laplace Transform to find the solution.
We apply the Laplace transformation to each member of the differential equation
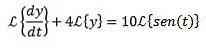
For the property of the derivative transformation we have
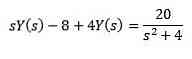
By developing all of Dan’s expressions and clearing, we are left behind
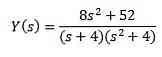
Using partial fractions to rewrite the right side of the equation we get
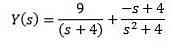
Finally, our goal is to find the function y (t) that satisfies the differential equation. Using the Laplace inverse transformation gives us the results
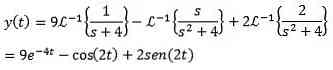
Example 2
break it
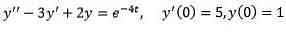
As in the previous case, we apply transformations on both sides of the equation and separate terms with terms.
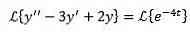
In this way we have the results
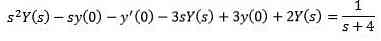
Replace with the initial value given and delete Y (s)
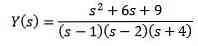
Using simple fractions, we can rewrite the equation as follows
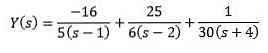
And applying the inverse transformation from Laplace gives us the results
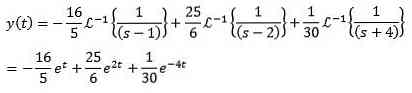
In these examples one can arrive at the wrong conclusion that this method is not much better than the traditional method for solving differential equations.
The advantage offered by Laplace transform is that there is no need to use parameter variations or worry about various instances of the indefinite coefficient method.
Besides solving the initial value problem with this method, from the beginning we used the initial conditions, so there was no need to do other calculations to find a particular solution.
System of differential equations
Laplace transform can also be used to find solutions for simultaneous ordinary differential equations, as the following example shows.
Example
break it
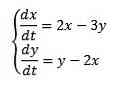
With initial conditions x (0) = 8 e and (0) = 3.
If you have to
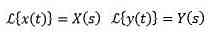
Then
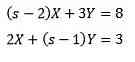
Complete the results in us
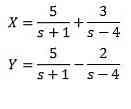
And when applying Laplace’s inverted transformation we have
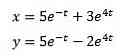
Mechanical and electrical circuits
Laplace transform is very important in physics, especially having applications for mechanical and electrical circuits.
A simple electrical circuit consists of the following elements
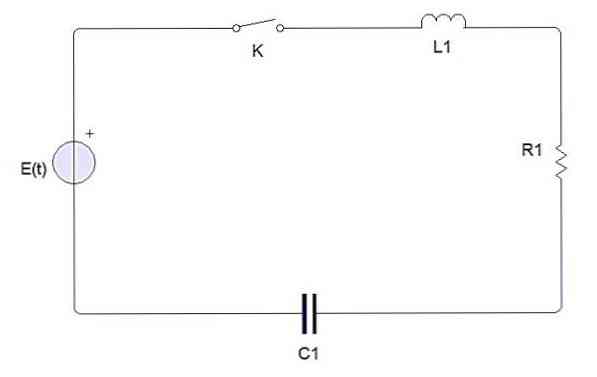
Switch, battery or source, inductor, resistor and capacitor. When the switch is closed, an electric current is generated which is denoted by i (t). The capacitor charge is denoted by q (t).
According to Kirchhoff’s second law, the voltage generated by source E to a closed circuit must be equal to the sum of each voltage drop.
Electric current i (t) is related to the charge q (t) in the capacitor by i = dq / dt. On the other hand, the voltage drop is defined for each element as follows:
The voltage drop across the resistor is iR = R (dq / dt)
The voltage drop in an inductor is L (di / dt) = L (d 2 q / dt 2 )
The voltage drop across the capacitor is q / C
With this data and applying the second Kirchhoff law to a simple closed circuit, a second-order differential equation is obtained which describes the system and allows us to determine the value of q (t).
Example
The inductor, capacitor, and resistor are connected to battery E, as shown in the picture. Inductors are 2 henries, 0.02 farad capacitors and 16 onhm resistance. When t = 0 the circuit is closed. Find the load and current at any time t> 0 if E = 300 volts.
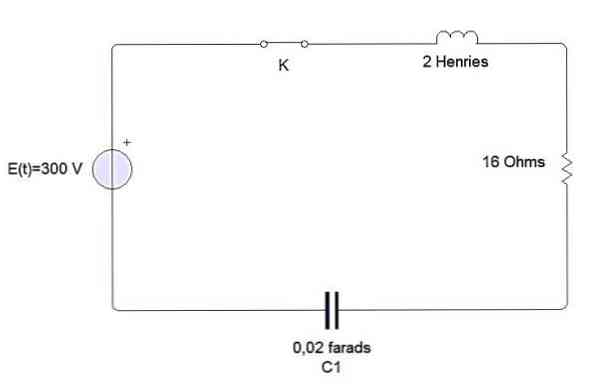
We have a differential equation that illustrates this circuit as follows
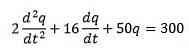
Where the initial conditions are q (0) = 0, i (0) = 0 = q ‘(0).
Applying the Laplace transformation we got that
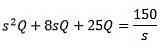
And clearing Q (t)
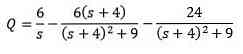
Then, apply the Laplace inverse transformation that we have