they are collinear vectors. They are one of the three types of vectors that exist. It’s about vectors that are in the same direction or line of action. This means the following: two or more vectors will be linear if arranged in a straight line parallel to each other.
A vector is defined as the amount applied to an object and is characterized as having direction, taste, and scale. Vectors can be found on planes or in space and can be of various types: collinear vectors, concurrent vectors and parallel vectors.

Index
- 1 choline vector
- 2 Characteristics
- 2.1 Example 1
- 2.2 Example 2
- 2.3 Example 1
- 3 multilevel vector system
- 3.1 Collinear vectors with opposite senses
- 3.2 Collinear vectors with the same meaning
- 3.3 Vector collectors with the same magnitude and opposite senses
- 4 Difference between collinear and concurrent vectors
- 5 References
Collinear vector
A vector is linear if the line of action of one vector is exactly the same as the line of action of all other vectors, regardless of the size and taste of each vector.
Vectors are used as representations in different fields such as mathematics, physics, algebra and also in geometry, where vectors are collinear only when the directions are the same, regardless of what they mean.
Feature
– Two or more vectors are linear if the relationships between coordinates are the same.
Example 1
We have a vector m = m_x; m_y and n = n_x; n_y. This is collinear if:
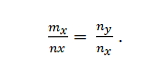
Example 2
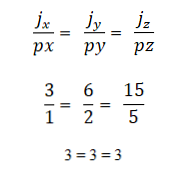
– Two or more vectors are linear if the product or vector product is zero (0). This is because, in the coordinate system, each vector is characterized by its coordinates, and if these are proportional to each other, the vectors will be linear. This is expressed as follows:
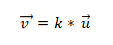
Example 1
We have vectors a = (10, 5) and b = (6, 3). To determine whether they are collinear, a determining theory is applied, which establishes the equality of cross products. That way, you have to:
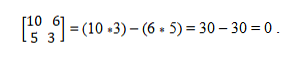
Colinear vector system
Colinear vectors are represented graphically using the direction and taste of this – considering that they must pass through the application-point and module, which are of a certain scale or length.
Kolinear vector system is formed when two or more vectors work on an object or objects, represent a force and act in the same direction.
For example, if two collinear forces are applied to objects, the result of this will only depend on the direction in which they act. There are three cases, namely:
Collinear vector with opposite senses
The results of two collinear vectors are equal to this number:
R = Σ F = F 1 + F 2.
Example
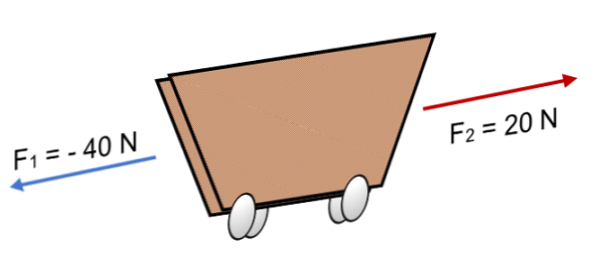
If two forces act on the train F 1 = 40 N and F 2 = 20 N in the opposite direction (as shown in the figure), the result is:
R = Σ F = (- 40 N) + 20N.
R = – 20 N.
Collinear vectors with the same meaning
The magnitude of the resultant force will be equal to the sum of the collinear vectors:
R = Σ F = F 1 + F 2.
Example
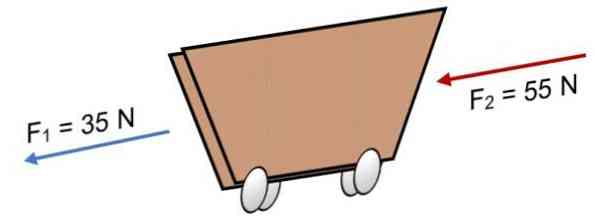
If two forces act on the train F 1 = 35 N and F 2 = 55 N in the same direction (as shown in the figure), the result is:
R = Σ F = 35 N + 55N.
R = 90 N.
Positive results indicate that the collinear vector is working to the left.
Spinal vector with the same magnitude and opposite senses
The result of the two collinear vectors will be the same as the sum of the collinear vectors:
R = Σ F = F 1 + F 2.
Because the force has the same magnitude but in the opposite direction – that is, one will be positive and the other negative -, when adding two forces the result will be zero.
Example
If two forces act on the train F 1 = -7 N and F 2 = 7 N, which have the same magnitude but in the opposite direction (as shown in the figure), the result is:
R = Σ F = (-7 N) + 7N.
R = 0.
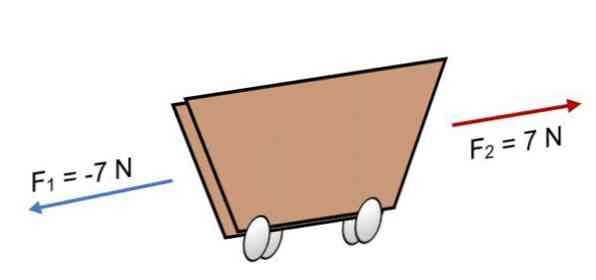
Because the resultant is equal to 0, it means that the vectors are balanced with each other and, therefore, the body is in equilibrium or rest (it will not move).
Difference between colinear and concurrent vectors
Collinear vectors are characterized by having the same direction on the same line, or because they are parallel to the line; that is, they are direct parallel line vectors.
On the other hand, concurrent vectors are defined because they are in different action lines that are intercepted in one point.
In other words, they have the same origin or arrival – regardless of their module, direction or direction -, forming an angle between them.
Concurrent vector systems are solved by mathematical or graphical methods, which are the force parallelogram method and the polygon force method. Through this the resulting vector value will be determined, which shows the direction in which the body will move.
Basically, the main difference between collinear vectors and concurrent vectors is the line of action in which they act: the collinear acts in the same line, while being concurrent on various.
That is, collinear vectors act in one plane, “X” or “Y”; and concurrent actions on both planes, starting from the same point.
Collinear vectors are not at one point, as are the same times, because they are parallel with each other.
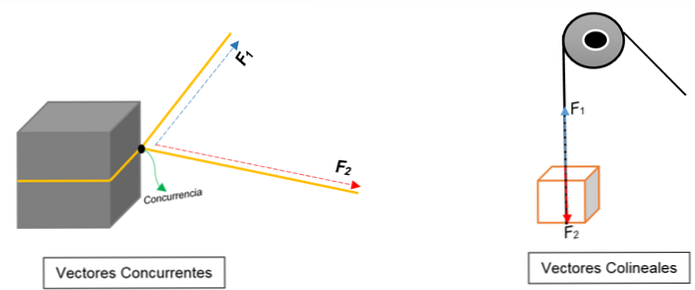
In the left image you can see a block. Tied with a rope and a knot dividing it into two; when pulled in different orientations and with different strengths, the blocks will move in the same direction.
Two vectors are represented that agree in a point (block), regardless of module, understanding or direction.
Conversely, in the right picture appears a pulley that lifts the box. The rope represents the line of action; when drawn, two forces (vectors) act on it: one tension force (when climbing a block) and another, the force that exerts the weight of the beam. Both have the same direction but in the opposite direction; don’t agree on one thing.