Isosceles triangle features, formulas and area, calculations

A isosceles triangle This is a three sided polygon, where two of them have the same size and the third side has a different size. This last side is called the base. Because these characteristics are given this name, which in Greek means “same foot”

Triangles are polygons that are considered the simplest in geometry, because they are formed by three sides, three angles and three vertices. They are those that have the fewest edges and angles with respect to other polygons, but their use is very broad.

Index

• 1 Characteristics of isosceles triangle
  • 1.1 Components
• 2 Properties
  • 2.1 Internal angle
  • 2.2 Number of sides
  • 2.3 Congruent side
  • 2.4 Congruent angles
  • 2.5 Height, median, bisector and bisector are coincidences
  • 2.6 Relative height
  • 2.7 Orthocenter, barycenter, incenter and circumcenter coincide
• 3 How to calculate the perimeter?
• 4 How to calculate height?
• 5 How to calculate the area?
• 6 How to calculate the base of a triangle?
• 7 Exercises
  • 7.1 First exercise
  • 7.2 The second exercise
  • 7.3 Third exercise
• 8 References

Characteristics of isosceles triangle

Isosceles triangles are classified using the size of their sides as parameters, because the two sides are congruent (having the same length).

According to the internal angle amplitude, isosceles triangles are classified as:

• Rectangle isosceles triangle : two sides are the same. One of the angles is straight (90 ^o ) and the other is the same (45 ^o each)
• Triangular obtuse isosceles angle : two sides are the same. One corner is blunt (> 90 ^o ).
• Isosceles acute triangle elbows : the two sides are the same. All angles are sharp (<90 ^o ), where two have the same size.

Component

• Median : is a line coming out of the midpoint of one side and reaching the opposite point. Three medians agree on a point called centroid or centroid.
• The bishop : is a ray which divides the angles of each angle into two angles of the same size. That is why it is known as the symmetry axis and this type of triangle has only one.
• Mediatrix : is a segment perpendicular to the side of the triangle, which originates from this center. There are three mediations in the triangle and they agree at a point called circuncentro.
• Height : is the line that moves from the point to the opposite side and also this line is perpendicular to that side. All triangles have three heights, which coincide at a point called the orthocenter.

Property

Isosceles triangles are defined or identified because they have several properties that represent them, derived from the theorems put forward by great mathematicians:

Internal angle

The number of internal angles is always equal to 180 ^o .

Number of sides

The number of two-sided steps must always be greater than the size of the third side, a + b> c.

Congruent side

Isosceles triangle has two sides with the same size or length; that is, they are congruent and third parties different from this.

Congruent angle

Isosceles triangle is also known as iso-angular triangle too, because they have two angles that have the same size (congruent). This is located at the base of the triangle, opposite to the side that has the same length.

Because of this, the theorem that establishes that:

“If a triangle has two sides that are congruent, the angle opposite to that side will also be congruent.” Therefore, if an isosceles triangle the angle of its base is congruent.

Example:

The following image shows ABC triangles. By tracing the bisector of the angle of angle B to the base, the triangle is divided into two triangles equal to BDA and BDC: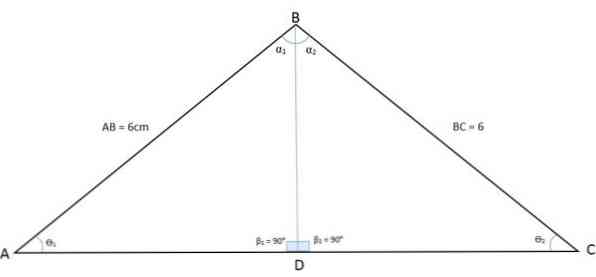

Thus, the angle of node B is also divided into two equal angles. The bisector is now the common side (BD) between the two new triangles, while the sides AB and BC are congruent. So you have cases of congruence, angles, sides (LAL).

This shows that the angles from angles A and C are the same size, as it can also be shown that because the triangles BDA and BDC are congruent, the AD and DC sides are also congruent.

Height, median, bisector and bisector are coincidences

The line drawn from the point opposite the base to the midpoint of the base of the isosceles triangle, at the same time the height, median and bisector, and bisector relative to the opposite angle from the base ..

All of these segments coincide with the one that represents them.

Example:

The following figure shows an ABC triangle with a midpoint M that divides the base into two BM and CM segments.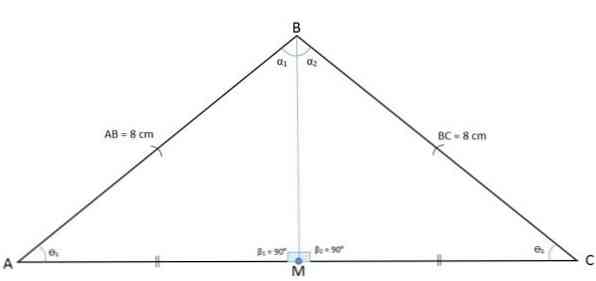

When you draw a segment from point M to the opposite point, by definition you get the median AM, which is relative to point A and the BC side.

Because the AM segment divides the triangle ABC into two equal triangles AMB and AMC, it means that the case of sides, angles, side congruence will be taken and therefore AM will also be a BÂC collector.

That is why the bishop will always be the same as the median and vice versa.

The AM segment forms an angle that has the same size for the AMB and AMC triangles; that is, they complement each other in such a way that each size will:

Med (AMB) + Med. (AMC) = 180 ^o

2 _* Med. (AMC) = 180 ^o

Med (AMC) = 180 ^o ÷ 2

Med (AMC) = 90 ^o

It can be seen that the angle formed by the AM segment is related to the base of a straight triangle, which indicates that this segment is really perpendicular to the base.

Therefore representing height and bisector, knowing that M is the midpoint.

Therefore AM straight lines:

• Represents the height of BC.
• It is.
• It is contained in mediatrix BC.
• This is the line for the vertex angle

Relative height

The height, which is relative to the same side, has the same size too.

Because the isosceles triangle has two equal sides, the two heights will also be the same.

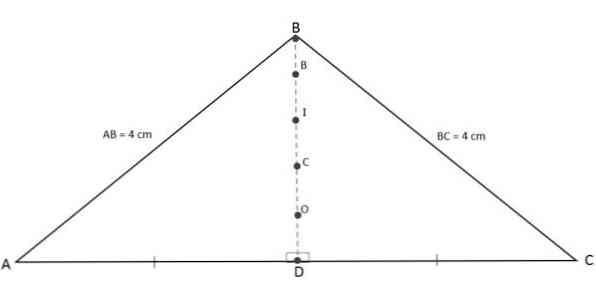
Orthocenter, barycenter, incenter and circumcenter together

Because height, median, bisector and lines relative to the base are represented at the same time by the same segment, the orthocenter, centrocentric incenter and circumenter will be collinear points, i.e. they will be on the same line:

How to calculate the perimeter?

Polygon perimeter is calculated by the number of sides.

As in this case the isosceles triangle has two sides of the same size, the perimeter is calculated by the following formula:

P = 2 _* (side a) + (side b).

How to calculate height?

Its height is a line that is perpendicular to its base, dividing the triangle into two equal parts by extending to the opposite point.

The height represents the opposite leg (a), half of the base (b / 2) to the adjacent foot and the “a” side represents the sloping side.

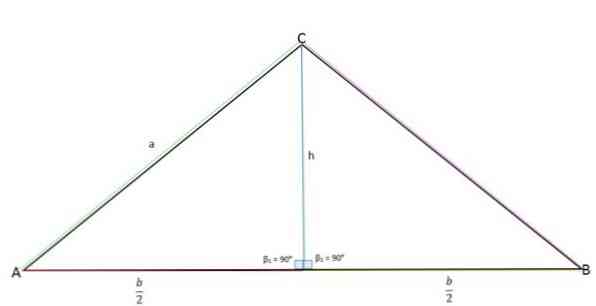
Using the Pythagorean theorem, you can determine the height value:

a ² + b ² = c ²

Where:

a ² = height (h).

b ² = b / 2.

c ² = side a.

Substitute these values ​​in the Pythagorean theorem, and clean up the height we have:

h ² + ( b / 2) ² = a ²

h ² + b ^2/4 = a ²

h ² = a ² – b ² /4

h = √ ( a ² – b ^2/4 ).

If the angle formed by the congruent side is known, the height can be calculated by the following formula:

How to calculate area?

The area of ​​a triangle is always calculated with the same formula, multiplying the base by height and dividing by two:

There are cases where only the measurement of two sides of a triangle and the angle formed between them are known. In this case, to determine the area it is necessary to apply trigonometric ratios: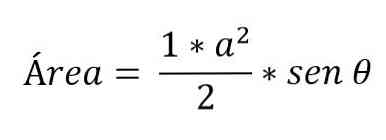

How to calculate the base of a triangle?

Because the isosceles triangle has the same two sides, to determine the value of the base must be known at least the height or one of its angles.

Know the height of the Pythagorean theorem used:

a ² + b ² = c ²

Where:

a ² = height (h).

c ² = side a.

b ² = b / 2, unknown.

We clean b ² formulas and we have to:

b ² = a ² – c ²

b = √ a ² – c ²

Because this value corresponds to half of the base, it must be multiplied by two to get the complete size of the base of the isosceles triangle:

b = 2 _* (√ a ² – c ² )

In the case that only the same side values ​​and angles between the two are known, trigonometry is applied, tracing a line from the point to the base dividing the isosceles triangle into two right triangles.

In this way, half of the basis is calculated by:

It is also possible that only the height and angle values ​​of points that are opposite to the base are known. In that case base trigonometry can be determined:

practice

First exercise

Find the area of ​​the isosceles triangle ABC, knowing that the two sides are 10 cm in size and the third side is 12 cm.

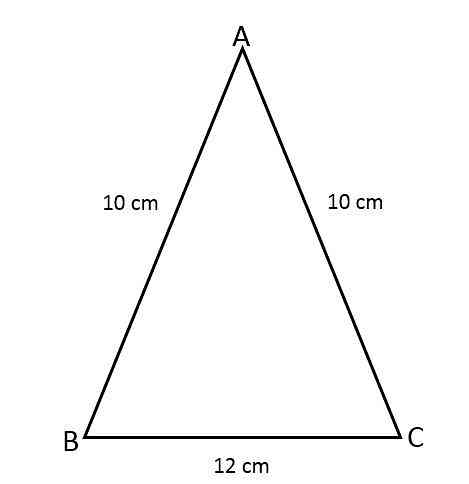
The solution

To find the area of ​​a triangle it is necessary to calculate the height using the area formula related to the Pythagorean Theorem, because the value of the angle formed between the same side is unknown ..

We have the following isosceles triangle data:

• The same side (a) = 10 cm.
• Base (b) = 12 cm.

Value in formula replaced:

Second exercise

The lengths of the two equal sides of the isosceles triangle are 42 cm, the joining of these sides forms an angle of 130 ^o . Determine the value of the third side, the area of ​​the triangle and the circumference.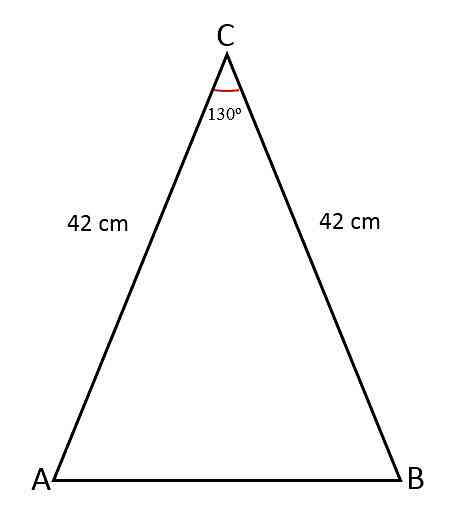

The solution

In this case measurements of the sides and angles between the two are known.

To find out the missing side value, which is the base of the triangle, a line is drawn perpendicular to it, dividing the angle into two equal parts, one for each right triangle formed.

• The same side (a) = 42 cm.
• Angle (Ɵ) = 130 ^o

Now with trigonometry the value of half of the base is calculated, which corresponds to half of the hypotenuse:

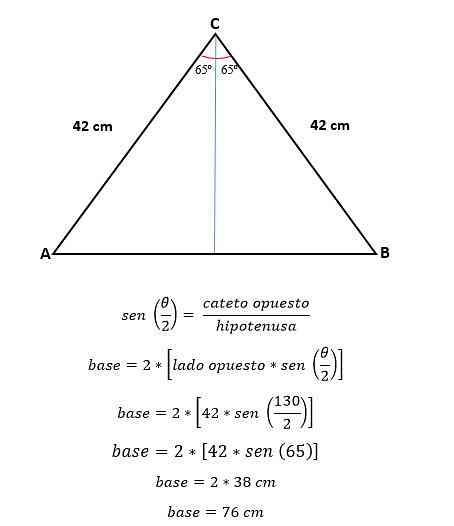
To calculate the area, we need to know the height of the triangle which can be calculated with trigonometry or with the Pythagorean theorem, now the base value has been determined ..

With trigonometry it will become:

Perimeter calculated:

P = 2 _* (side a) + (side b).

P = 2 _* (42 cm) + (76 cm)

P = 84 cm + 76 cm

P = 160 cm.

Third exercise

Calculate the internal angle of an isosceles triangle, knowing that the base angle is = 55 ^o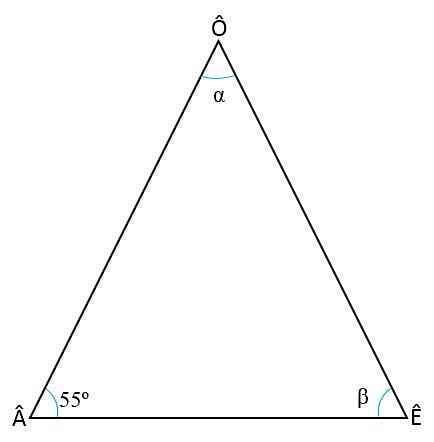

The solution

To find the two missing angles (Ê and Ô) it is necessary to remember two triangle properties:

• The number of internal angles for each triangle will always be = 180 ^o :

 + Ê + Ô = 180 ^o

• In an isosceles triangle, the base angles are always congruent, that is, they have the same size, therefore:

 = Ô

Ê = 55 ^o

To determine the angle value Ê, replace the value from another angle in the first rule and delete Ê:

55 ^o + 55 ^o  + Ô = 180 ^o

110 ^o + Ô = 180 ^o

Ô = 180 ^o – 110 ^o

Ô = 70 ^o .

Reference

1. Álvarez, E. (2003). Geometry elements: with a lot of practice and compass geometry. University of Medellín.
2. Vlvaro Rendón, AR (2004). Technical Drawing: activity notebook.
3. Angel, AR (2007). Pearson’s Basic Algebra Education.
4. Arthur Goodman, LH (1996). Algebra and trigonometry with analytic geometry. Pearson Education.
5. Baldor, A. (1941). Havana Algebra: Culture.
6. José Jiménez, LJ (2006). Mathematics 2.
7. Tuma, J. (1998). Engineering Mathematics Handbook. Wolfram MathWorld.